|
CURIOUS PROPERTIES OF
153 |
References about number 153 can be found in the New Testament,
where in the net Simon Peter drew from the Sea of Tiberias held 153 fishes. Some
of the interesting properties of number 153 published in [1] are:
Curious properties of number 153:
- It is the smallest number which can be expressed as the sum
of cubes of its digits:
153 = 13 + 53 +
33
- It is equal to the sum of factorials of number from 1 to
5:
153 = 1! + 2! + 3! + 4! + 5!
- The sum of digits of 153 is a perfect square:
1 + 5 + 3 = 9 = 32
- The sum of aliquot divisors of 153 is also a perfect
square:
1 + 3 + 9 + 17 + 51 = 81 =
92
Aliquot divisors of a number are all the divisors of that number
excluding the number itself but including 1. It is seen that the sum of aliquot
divisors of 153 is the square of the sum of the digits of 153.
- On adding the number 153 to its reverse,504 is obtained, whose square is the
smallest square which can be expressed as the product of two different non-square numbers
which are reverse of one another:
153 + 351 = 504
5042 = 288 x 882
- It can be expressed as the sum of all integers from 1 to 17.
In other words, 153 is the 17th
triangular number. Since reverse of 153, i.e. 351 is also
a triangular number, 153 can be termed as a reversible triangular number.
- Number 153 is also a Harshad
number(also called Niven number), i.e. it is divisible by the sum of
its own digits:
153 / (1 + 5 + 3) = 17
Since reverse of 153, i.e. 351 is also a Harshad number(or Niven Number), 153
can be termed as a reversible Harshad
number(or reversible Niven Number).
- It can be expressed as the product of two numbers formed from
its own digits:
153 = 3 * 51
Note that the digits used in multipliers are same as in
product.
- The number 135, which is formed by rearranging the digits of
153, can be expressed as:
135 = 11 + 32 + 53
- The sum of all divisors of 153 is 234.
1 + 3 + 9 + 17 + 51 + 153 = 234
The product of aliquot divisors of 153 is 23409:
1 * 3 * 9 * 17 * 51 = 23409
Note that the product of aliquot divisors of 153 contain the sum
of all divisors of 153 juxtaposed:
23409 = 234:09
234 = Sum of all divisors of 153
09 = Square root of the sum of aliquot divisors of
153.
- When the cubes of the digits of any number, that is, a
multiple of 3 are added, and then this process is repeated, the final result
is 153, where the process ends because 153 = 13 + 53 +
33
For example: Take the number 108
13 + 03 + 83 = 513 and 53 + 13 + 33 = 153
So, the number 108 reaches 153 in two cycles and it can be represented as
108→513→153
A detailed study of all numbers up to 105reveals that all numbers which are multiple of 3 and are less than 105 reach 153 (after the repeated process of summing the cubes of digits is done) in maximum 14 cycles. However, maximum 13 cycles is required for all numbers, which are multiple of 3 and are less than 10,000.
The smallest number, which requires 13 cycles to reach 153, is 177, i.e.,
177→ 687→ 1071→345→
216→ 225→ 141→ 66→ 432→
99→ 1458→ 702→ 351→ 153
Table 1 indicates the smallest numbers, which reach 153 in
cycles from 1 to 14.
TABLE: 1
|
No. of cycles |
Smallest number |
|
1 |
135 |
|
2 |
18 |
|
3 |
3 |
|
4 |
9 |
|
5 |
12 |
|
6 |
33 |
|
7 |
114 |
|
8 |
78 |
|
9 |
126 |
|
10 |
6 |
|
11 |
117 |
|
12 |
669 |
|
13 |
177 |
|
14 |
12558 |
The Smallest Number (Of course a multiple of 3) which reaches 153 in 15 cycles is
44499999999999999999, which in short can be represented as 43917 i.e.
44499999999999999999→ 12585→ 771→687 → 1071→ 345→216→ 225→ 141→ 66→ 432→ 99→ 1458→ 702→ 351→ 153
Jörg Zurkirchen vide his email dated 16th aug 2021 advised that Jon E. Schoenfield found the smallest numbers, which reach 153 in 16 and 17 cycles (Sloane's A346630).
a(16) = 3.777999...999*10^61042524005486970; it has one 3, three 7's, and 61042524005486967 9's, so the sum of the cubes of its digits is 1*33 + 3*73 + 61042524005486967*93 = 44499999999999999999 = a(15).
a(17) consists of the digit string 45888 followed by a very, very long string of 9's. The number of 9's in that string is (a(16) - 1725)/729,
which is a 61042524005486968-digit number consisting of the digit 5 followed by 753611407475147 copies of the 81-digit string
182441700960219478737997256515775034293552812071330589849108367626886145404663923 followed by a single instance of the 60-digit string
182441700960219478737997256515775034293552812071330589849106
He also shows how to find additional numbers (Sloane's A346789).
Some New Observations on number
153:
- If p(x) represents the number of primes
up to x, then the following holds good:
p (153) = p (15) *
3!
- For a beautiful fascinating observation in reciprocal of 153
by Patrick De Geest,
click here.
- 153153 is the
smallest odd abundant number ending in 3.(added on 31-12-2001)
- 153153, 351351, 513513 are all odd abundant numbers.(added on 31-12-2001)
- One of our books of sacred writings is titled The Hidden
Words. It is a collection of short meditations, divided into two sections. The
first section contains 71 items that were revealed
in Arabic; the second section of 82 items was
revealed in Persian (Farsi). I think you see my point already..... 71 + 82 = 153. I have often told my fellow believers about this
connection between math and our Faith's literature. They are always quite
impressed, to say the least.(Sent by Terry Trotter by
email dt 25th Dec, 2001)
-
Let us say 153 increasingly from left to right:
1, 15, 153
We find that 115153 is prime?(Sent by G.L.Honaker,Jr. by email dt 3rd Feb, 2002)
- The square root of 153 (i.e. 12.369) is the amount of full moons in one year. (Sent by James Furia by
email dt 16th June, 2009)
- The length of the grand gallery inside the Great Pyramid is 153 feet. (Sent by James Furia by
email dt 16th June, 2009)
- Binary presentation i.e. 10011001 and hexadecimal presentation i.e. 99 of 153 are palindromes.
(Sent by
Lauri.Kukko@ilkka-yhtyma.fi by
email dt 29th May, 2010)
- Within the Great Pyramid, from the King's Chamber floor up to the summit
platform there are 153 courses of masonry (From the Pyramidology Book #1 by
Adam Rutherford).
(Sent by Joe Biddy by
email dt 1st October, 2010)
- (11 + 55 + 33) mod 1000 = 153
(Sent by M Sihabudin, from Indonesia)
- If you add the highest and lowest number from these six
135 + 531
153 + 513
315 + 351
you will get 666 - an important number in the book of revelation.
(Sent by Bjorn Jonasson from Sweden by email dated 01 Jul 2011)
- 153 is the smallest number k, such k4could be split into two primes in two different ways:
1534 = 547981281 and 547981281 can be split into :
5479 , 81281 and 5 , 47981281
(Sent by Claudio Meller by email dated 26 May, 2012)
- There are 153 days in any five consecutive months not containing February.
- cos513 = cos(360+153) = cos153 (Sent by LEONIDAS PATSURAKOS by email dated 6 Sept, 2013)
- The sum of first 8 Heegner numbers ( All Heegner numbers less than 153) is = 1 + 2 + 3 + 7 + 11 + 19 + 43 + 67 =153
(Sent by Hanson Chen by
email dt 19 June, 2015)
- The Curious properties of the binary representation of 153
A less described feature of 153 emerges if the number is read as a binary number: 10011001
10011001 when viewed linear is a palindrome comprising 8 positions. If 10011001 is circularized,
forming an octagonal ring,
more patterns emerge.
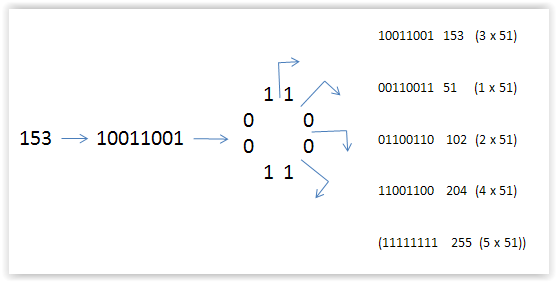
Note that the maximal number in a byte (255) is included in above figure.
The circularized 10011001 sequence gives a multiple of 51 (or 3 x 17) from any position the sequence is read.
(Sent by Stefan Krauss, University of Oslo by email dated 29 August 2017)
If you find any new and interesting observation
about 153, please email me.
---------------------------------------------------------------------------
[1] Curious Properties of 153, Shyam Sunder
Gupta, Science Reporter, February 1991, India.
Back
Home
